The previous post introduced the notion of a stopping time . A stochastic process
can be sampled at such random times and, if the process is jointly measurable,
will be a measurable random variable. It is usual to study adapted processes, where
is measurable with respect to the sigma-algebra
at that time. Then, it is natural to extend the notion of adapted processes to random times and ask the following. What is the sigma-algebra of observable events at the random time
, and is
measurable with respect to this? The idea is that if a set
is observable at time
then for any time
, its restriction to the set
should be in
. As always, we work with respect to a filtered probability space
. The sigma-algebra at the stopping time
is then,
The restriction to sets in is to take account of the possibility that the stopping time can be infinite, and it ensures that
. From this definition, a random variable
us
-measurable if and only if
is
-measurable for all times
.
Similarly, we can ask what is the set of events observable strictly before the stopping time. For any time , then this sigma-algebra should include
restricted to the event
. This suggests the following definition,
The notation denotes the sigma-algebra generated by a collection of sets, and in this definition the collection of elements of
are included in the sigma-algebra so that we are consistent with the convention
used in these notes.
With these definitions, the question of whether or not a process is
-measurable at a stopping time
can be answered. There is one minor issue here though; stopping times can be infinite whereas stochastic processes in these notes are defined on the time index set
. We could just restrict to the set
, but it is handy to allow the processes to take values at infinity. So, for the moment we consider a processes
where the time index
runs over
, and say that
is a predictable, optional or progressive process if it satisfies the respective property restricted to times in
and
is
-measurable.
Lemma 1 Let
be a stochastic process and
be a stopping time.
- If
is progressively measurable then
is
-measurable.
- If
is predictable then
is
-measurable.
Proof: If is progressive then, as proven in the previous post, the stopped process
is also progressive and, hence, is adapted. It follows that
is
-measurable which, from the definition above, implies that
is
-measurable.
Furthermore, is
-measurable and is zero when restricted to the set
for all
, so is also
-measurable.
Now, consider a predictable process . Write
for the predictable sigma-algebra on
. That is, the subsets of
which are predictable when restricted to
and such that
is
-measurable. Then,
is
-measurable. By the functional monotone class theorem, it is enough to prove the result for processes of the form
for some pi-system of sets generating
.
The predictable sigma algebra is generated by the sets of the following forms,
-
for times
and
. If
then
which, by definition, is
-measurable.
-
for
. If
then
which is
-measurable, and so is also
-measurable.
⬜
So, the `adaptedness’ of measurable processes extends to stopping times. In fact, it is possible to go further and use this as an alternative definition of these sigma-algebras.
Lemma 2 Let
be a random variable and
be a stopping time. Then,
is
-measurable if and only if
for some progressively measurable (or, optional) process
.
is
-measurable if and only if
for some predictable process
.
Proof: If is
-measurable, then the process
is adapted and right-continuous. Therefore, it is optional (and hence, progressive) and clearly
.
For the second statement, consider the set of random variables which can be expressed as
for a predictable process
. The functional monotone class theorem can be used to show that
contains all
-measurable random variables. First,
is clearly closed under taking linear combinations. Second, if
is increasing to the limit
then there exists predictable processes
with
. Then,
is also in
.
Finally, it just needs to be shown that for all
in a pi-system generating
. By definition, the following sets generate
.
-
. In this case,
with
.
-
for
and
. Then,
with
.
In both these cases, is left-continuous and adapted and, hence, is predictable. ⬜
This result gives the main motivation for the definitions of and
. For the remainder of this post, I state and prove several simple results which are useful for general applications of stopping times.
Lemma 3 Any stopping time
is both
and
-measurable.
Proof: The deterministic process is trivially adapted and both left and right-continuous, so it is predictable and optional. Consequently, by the previous lemma,
is
and
-measurable. ⬜
Next, the sigma-algebras are increasing in the sense that we would hope.
Lemma 4 For any stopping time
,
If
is any other stopping time then,
If, furthermore,
whenever
then
.
Proof: This proof makes use of Lemma 2. First, by the lemma, every -measurable set
can be written in the form
for a predictable process
. However, as predictable processes are progressive,
will also be in
.
Now suppose that is
(resp.
) measurable. Then, there is a progressive (resp. predictable) process satisfying
. As the stopped process
is also progressive (resp. predictable) it follows that
is
(resp.
)-measurable.
Finally, suppose that whenever
and that
. Then
is a left-continuous and adapted at finite times, and is
-measurable. Hence, it is predictable process and
is
-measurable. ⬜
The sigma-algebras satisfy the expected left and right-limits. In the following lemma, the first statement says that right-continuity of a filtration extends to arbitrary stopping times. The second says that can indeed be interpreted as a left-limit. However, this statement does not say anything much for arbitrary stopping times, because it is not in general possible to strictly approximate them from the left in this way. If such a sequence
does indeed exist then the stopping time is called predictable.
Lemma 5 Let
be stopping times. Then
- If the filtration
is right-continuous and
for each
then
- If
, with a strict inequality whenever
, then
Proof: Starting with the first statement, we know that . So, it just needs to be shown that any
is in
. Any such set satisfies
Then, by right-continuity of the filtration, for any
as required.
For the second statement, we know that , so it is only necessary to prove that there is a generating set for
lying in
. As
it is enough to consider sets of the form
for
. However
as required. ⬜
As should be the case, the definition of the sigma-algebras at a constant stopping time is consistent with the filtration.
Lemma 6 If
is equal to the constant value
then,
Proof: If then for all times
,
showing that . Conversely, if
then
as required.
This shows that . The equality
follows by taking left limits and applying the previous lemma. ⬜
Given two stopping times it follows from the definitions that
and
. So,
is in
and, by symmetry, is also in
. Furthermore, these two sigma-algebras coincide when restricted to this set. For a sigma-algebra
on
, and a subset
, we use
to denote the sigma-algebra on S consisting of sets
for
.
Lemma 7 If
are stopping times then
Proof: If is
measurable then
is in
and
. The reverse inclusion follows by exchanging
and
.
Next, is generated by sets in
, and by sets of the form
for
which, restricted to
, coincide with
. So,
, and the reverse inclusion follows by exchanging
and
. ⬜
Given a stopping time taking values in a countable set of times, the following result is often useful to show that a set is in the sigma algebra by checking it at each of the fixed times.
Lemma 8 Let
be stopping times such that
for all
.
A set
is in
if and only if
for each
.
Proof: By the previous lemma, if then
. Conversely,
as required. ⬜
Finally, the following result is used to construct new stopping times out of old ones. If we wait until a time occurs, and then decide to either use that time or not based on an
-measurable event, the result is again a stopping time.
Lemma 9 Let
be a stopping time and
. Then,
is also a stopping time.
Proof: This follows from the following
for all . ⬜
Dear Almost sure,
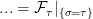
In lemma 7, do you want to show
Thanks
Yes! I’ll fix it. Thanks
Dear Georges, ?
?
Excuse me if I am wrong, but in the proof of Lemma 2, last but one line, shouldn’t it be
You’re right. I fixed it, thanks.
Thanks for your answer. Did you also by any chance see my question on the Stochastic Integral ?
Hello George,
I recently meet the problem on consistency of probability measures. Given a sequence of probability measures Q_n, how is it possible to check that they are consistent? The definition seems impractical. What I want is a method that we can actually apply facing concrete examples. Also, where shall I start if I want to find counter-examples?
Thank you very much!
Hi, I am struggling with the definition of the “stopping-time sigma-algebra” (aka sigma algebra at stopping time). You state that, “The idea is that if a set is observable at time
is observable at time  then for any time
then for any time 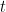 , its restriction to the set
, its restriction to the set 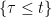 should be in
should be in 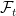 .” Is it possible to get a concrete example please? Thanks.
.” Is it possible to get a concrete example please? Thanks.
Hi, Thanks for the excellent posts. One question: Why is the sigma algebra at a stopping time “tau” not defined as the sigma algebra generated by tau, in the first place? How is this notion related to the (standard) definition that you have given above? I vaguely recall some mention (not sure in which reference) that the former definition is not operationally useful to perform the related analysis–is that so or are there other reasons?
Consider the case where is constant, equal to a deterministic time
is constant, equal to a deterministic time  . Then
. Then  . With the definition you suggest,
. With the definition you suggest, 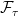 would be trivial. More generally, the sigma algebra generated by
would be trivial. More generally, the sigma algebra generated by  would miss out lots of events observable at the stopping time. We want
would miss out lots of events observable at the stopping time. We want 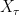 to be
to be 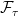 -measurable for any reasonably regular adapted process X.
-measurable for any reasonably regular adapted process X.
I have been trying to prove if and
and 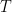 are stopping times and
are stopping times and 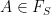 , then
, then 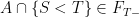 . Any suggestions on how to proceed?
. Any suggestions on how to proceed?
You can try using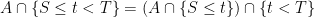 . From the definitions of the two sigma-algebras, this is in
. From the definitions of the two sigma-algebras, this is in  . Take the union over a countable dense set for t. Alternatively use the fact that
. Take the union over a countable dense set for t. Alternatively use the fact that 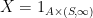 is left-continuous and adapted, so
is left-continuous and adapted, so 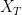 is
is 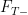 measurable.
measurable.
Nitpicking: “resp.” in Lemma 2 is quite confusing. Probably you meant just “or”? [GL: Fixed, thanks!]
Why is the “progressive” condition used to show that $X_\tau$ is $\mathcal F_\tau$-measurable? Is adapted $X$ not enough?
Dear George,
I believe there is a mistake in the last part of the proof of Lemma 4. The suggested process X is not left-continuous. Take s<= \sigma < t then X_t-X_s=0 while if \sigma<s<t then X_t-X_s=1. I also believe that in the second bullet point in the proof of Lemma 2, the inequality between s and t is in the wrong direction.
Nevermind the first comment, that is obviously left-continuity. I stand by the second comment nonetheless